An ever expanding collection of ML & DL terminologies
Table of Content
Loss Functions
MAE(Mean Absolute Error)MSE(Mean Squared Error)
RMSE(Root Mean Squared Error)
Cross Entropy
Activation Functions
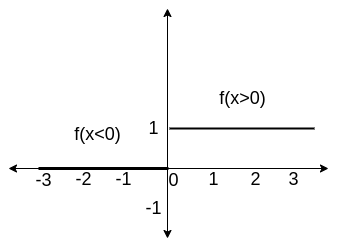
1 .Step Function
Equation for Step Function
\(f(x) =
\begin{cases}
0, & x \lt 0 \\
1, & x \geq 0
\end{cases}\)
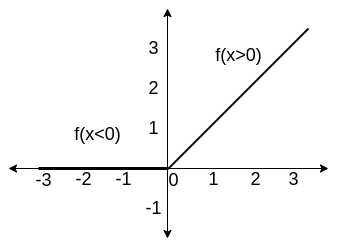
2. ReLU
Equation for Rectified Linear Unit(ReLU) activation function
\(f(x) =
\begin{cases}
0, & x \lt 0 \\
x, & x \geq 0
\end{cases}\)
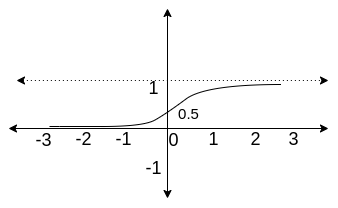
3. Sigmoid
Equation for Sigmoid
\(f(x) = \frac{\mathrm{1} }{\mathrm{1} + e^{-x} }\)
4. Tanh
Equation for Tanh \(f(x) = \frac{e^{x} - e^{-x} }{e^{x} + e^{-x} }\)
5. Leaky ReLU
Equation for Rectified Linear Unit(ReLU) activation function \(f(x) = \begin{cases} 0.01x, & x \lt 0 \\ x, & x \geq 0 \end{cases}\)
6. Softmax
The softmax function squashes the outputs of each unit to be between 0 and 1, just like a sigmoid function. But it also divides each output such that the total sum of the outputs is equal to 1. The output of the softmax function is equivalent to a categorical probability distribution, it tells you the probability that any of the classes are true. Simply speaking, it a generalization of the logistic function to multiple dimensions. \(\text{softmax}(\mathbf{z})_i = \frac{\exp(z_i)}{\sum_{l=0}^{K-1}\exp(z_l)}\)
Components of NN
1. Activation Function
Activation Functions determines the output of each element (perceptron or neuron) in the neural network. Each neuron’s output is the input of the neurons in the next layer of the network, so the inputs pass through multiple activation functions until the output layer gives a prediction.
2. Bias
Bias is a non-zero number defined by us and it acts the same way as \(c\) does in the equation \(y = m\times x + c\).
3. Neuron
A neuron is the most basic unit of a Neural Network. Each neuron stores information either as a real number or a mathematical operation that takes input, multiplies it by it’s weights and then passes the sum through the activation function to the other neurons.
4. Weights
Weights decide the importance of the input coming into a neuron. Weights are initialised randomly in the beginning, later however they are automatically calculated based on the output.
5. Loss function
It is a metric to know how well the algorithm fits on the given data. In other words, it gives us the error between the actual value and the predicted value. A Loss Function is defined for a single training example, whereas when used in context of whole dataset it’s called Cost Function, which is the average of Loss Functions. As a process of optimizing the model, we try to lowering the value of the loss function
6. Optimizer
Optimizers are algorithms which are used to update the weights based on the based on the errors calculated by the loss function. Essentially, the loss function is the guide telling the optimizer whether it is updating the weights correctly or not.
Loss Functions
1. Mean Absolute Error
The algorithm takes the differences in all of the predicted and actual value, adds them up and then divides them by the number of observations. Since it is the absolute value it doesn’t matter which way we take the difference. Simply put, the average difference observed in the predicted and actual values across the whole test set.
\[MAE =(\frac{1}{n})\sum_{i=1}^{n}\left | y_{i} - y_{i}' \right|\]2. Mean Squared Error
As the name suggests, we take average of squares between predicted and actual value, over the whole set. Now, as a result of the squaring, it assigns more weight to the bigger errors. The algorithm then continues to add them up and average them. Thus this isn’t the most useful algorithms in most cases, however, it is a stepping stone to RMSE.
\[MSE = (\frac{1}{n})\sum_{i=1}^{n}(y_{i} - y_{i}')^{2}\]3. Root Mean Squared Error
RMSE can be obtained just be obtaining the square root of MSE.
\[RMSE = \sqrt{(\frac{1}{n})\sum_{i=1}^{n}(y_{i} - y_{i}')^{2}}\]
